Scientific machine learning
I have been increasingly interested in ML/AI, particularly in integrating mathematical and physical structures into neural networks. Therefore, I mainly focus on structure-preserving ML. Scientific machine learning (SciML) offers a promising approach to tackling problems where traditional numerical algorithms fall short. For instance, when designed properly, SciML can provide an alternative method for studying dynamical systems.
The following structure-preserving SciML work has been primarily supported by DOE ASCR data-intensive scientific machine learning program.
Structure-preserving SciML work
The recent representative papers include: dynamics learning for multiscale and/or stiff ODEs1 2 3 and large-scale PDEs,4 learning flow maps for Hamiltonians 5 6, their applications,7 8 and molecular dynamics.9 10 Please refer to the corresponding references for more details.
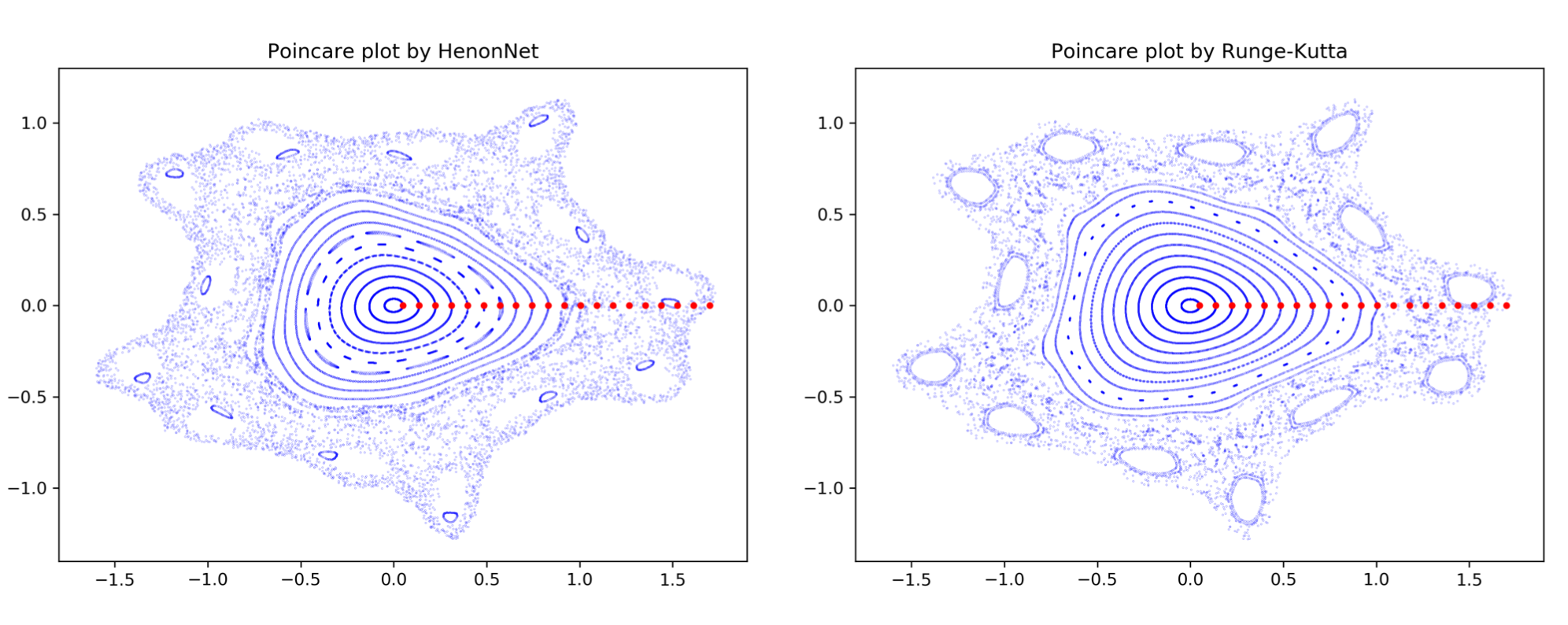
The following fusion ML work has been primarily supported by DOE FES SciDAC and FES AI/ML programs.
Fast ML-based surrogates for fusion modeling
We have developed novel symplectic neural network (HenonNet) and applied it as a fast surrogate to generate Poincaré plot for tokamaks.11 We also developed physics-assisted latent dynamics learning for collisional radiative models.12 13 Please refer to the corresponding references for more details.
-
D. Serino, A. Alvarez Loya, J. W. Burby, I. G. Kevrekidis, and Q. Tang. Fast-slow neural networks for learning singularly perturbed dynamical systems, Journal of Computational Physics, 537:114090, 2025. ↩
-
A. Alvarez Loya, D. Serino, J. Burby, and Q. Tang. Structure-preserving neural ordinary differential equations for stiff systems, submitted, 16 pages, 2025. ↩
-
Y. Lu, X. Li, C. Liu, Q. Tang, and Y. Wang. Learning generalized diffusions using an energetic variational approach, submitted, 23 pages, CiCP, 2024. ↩
-
A. J. Linot, J. W. Burby, Q. Tang, P. Balaprakash, M. D. Graham, and R. Maulik. Stabilized Neural Ordinary Differential Equations for Long-Time Forecasting of Dynamical Systems, Journal of Computational Physics, 474:111838, 2023. ↩
-
V. Duruisseaux, J. W. Burby, and Q. Tang. Approximation of Nearly-Periodic Symplectic Maps via Structure-Preserving Neural Networks, Scientific Reports, 13.1:8351, 2023. ↩
-
Y. Chen, W. Guo, Q. Tang, X. Zhong. Reduced-order modeling of Hamiltonian dynamics based on symplectic neural networks, submitted, 25 pages, 2025. ↩
-
E. G. Drimalas, F. Fraschetti, C.-K. Huang, and Q. Tang. Symplectic neural network and its applications to charged particle dynamics in electromagnetic fields, in revision, PoP, 16 pages, 2025. ↩
-
C.-K. Huang, Q. Tang, et al. Symplectic neural surrogate models for beam dynamics. Journal of Physics: Conference Series, 2687(6):062026, 2024. ↩
-
H. Tischler, W. Li, Q. Tang, D. Perez, and T. Vogel. Predicting atomistic transitions with transformers, submitted, 10 pages, 2025. ↩
-
S.-H. Wang, Y. Huang, J. M. Baker, Y.-E. Sun, Q. Tang, and B. Wang. A theoretically-principled sparse, connected, and rigid graph representation of molecules, International Conference on Learning Representations (ICLR), 2025. ↩
-
J. W. Burby, Q. Tang and R. Maulik. Fast neural Poincare maps for toroidal magnetic fields, Plasma Physics and Controlled Fusion, 63:024001, 2020. ↩
-
N. A. Garland, R. Maulik, Q. Tang, X.-Z. Tang and P. Balaprakash. Efficient data acquisition and training of collisional-radiative model artificial neural network surrogates through adaptive parameter space sampling, Machine Learning: Science and Technology, 3:045003, 2022. ↩
-
X. Xie, Q. Tang, and X.-Z. Tang. Latent space dynamics learning for stiff collisional-radiative models, Machine Learning: Science and Technology, 5:045070, 2024. ↩